Деление отрезка в данном отношении
Пусть даны точки A(x1;y1) и B(x2;y2). 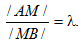
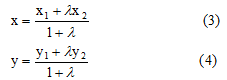
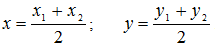
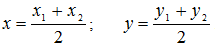
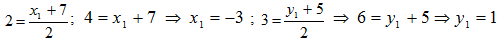
Координаты точки М(х,у), лежащей на отрезке АВ и делящей его в данном отношении:
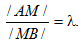
вычисляются по формулам:
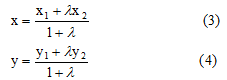
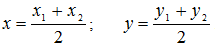
В частности, при 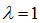 получаются формулы для координат середины отрезка:
получаются формулы для координат середины отрезка:
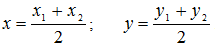
Пример 2. Известны точки A(-2;5), B(4;17)- концы отрезка [AB]. На этом отрезке находится точка М, расстояние которой от А в два раза больше расстояния от В. Определить координаты точки М.
Решение. Так как |AM|=2|MB|, то 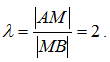 .
.
Здесь x1=-2, y1=5, x2=4, y2=17; следовательно, 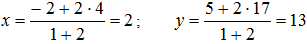 то есть M(2;13).
то есть M(2;13).
Пример 3. Точка M(2;3) служит серединой отрезка [AB]. Определить координаты точки А, если B(7;5).
Решение. Здесь x=2, y=3, x2=7, y2=5, откуда
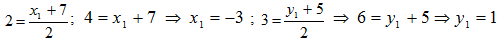
то есть A(-3;1)
|
|
 |
бредор 23.06.2011 20:41 хорошая инфа
|
Поиск на сайте
