Упорядоченная тройка некомпланарных векторов a, b, с с общим началом в точке О называется правой, если кратчайший поворот от вектора a к вектору b наблюдается из конца вектора с происходящим против движения часовой стрелки. В противном случае данная тройка называется левой (Рис.4).

Векторным произведением векторов 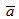и 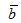называется вектор 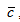, обозначаемый 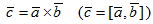, который удовлетворяет следующим трем условиям:

1. |c| = | a | |b| sin (a^b);
2. c ┴ a, c ┴ b;
3. тройка a, b, c – правая.

Основные свойства векторного произведения векторов:
1. a • b = - (b • a);
2. (λ a)*b= λ (a • b) = a •(λb);
3. a •(b+с) = a • b+ a • с;
4. a • b = 0, если a||b;
5. |a • b| = S, где S – площадь параллелограмма, построенного на векторах a и b, имеющих общее начало в точке φ. (см. рис. )

Если a =(x1, y1, z1), b =(x2, y2, z2), то векторное произведение 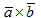выражается через координаты данных векторов a и b, следующим образом:

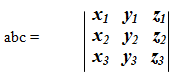
Пример 8. Даны векторы a = (1, 3, 1), b = (-2, 4, -1), c = (2, 4, -6). Требуется установить, компланарны ли данные векторы, в случае их некомпланарности выяснить, какую тройку (правую или левую) они образуют, и вычислить объем построенного на параллелипипеда.
Решение: Вычислим

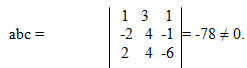
из значения смешанного произведения следует, что векторы некомпланарны, образуют левую тройку и V = 78.

Пример 9. Вычислить площадь параллелограмма, построенного на векторах a = 2i +3j, b = i -4j. Здесь i =(1, 0), j=(0, 1)- единичные векторы, взаимно перпендикулярны.
Решение: a*b = (2i +3j)*( i -4j) = 2i* i +3j*i -8 i *j-12j*j = -3i *j-8i *j = -11i *j = c;
Sпар. = |c| = 11|i*j| = 11*1*1Sinπ /2 = 11.

Пример 10. Показать, что векторы a = 2 i +5j+7k, b = i +j-k, c = i +2j+2k компланарны.
Решение: Если векторы a, b, c компланарны, то abc = 0.

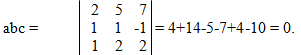
Векторы a, b, c компланарны.