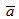Скалярным произведением двух векторов и 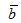называется число, обозночаемое 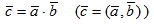и равное произведению модулей данных векторов на косинус угла между ними:

где (a^b) обозначает меньший угол между направлениями векторов a и b. Отметим, что всегда(0≤a^b≤π).

Основные свойства скалярного произведения векторов:
1. a •b = b• a;
2. (λa)•b= •(λb) = λ (a•b);
3. a•(b+с) = a•b+a•с;
4. a•b = | a | прa b = |b| прb| a |;
5. a • a = | a |²;
6. a • b = 0, если a ┴ b.

Если a =(x₁, y₁, z₁), b =(x₂, y₂, z₂), то в базисе (i, j, k):
a • b = x₁x₂+ y₁y₂ +z₁z₂, | a | = √x1²+ y1²+ z1², | b | = √x2²+ y2²+ z2².

Пример 6. Даны векторы a = λi+2j+3k, b = 4i + λj-4k. При каком значении λ эти векторы перпендикулярны?
Решение: Находим скалярное произведение этих векторов a•b = 4λ +2λ -12; так как a ┴ b, то a•b =0. отсюда 4λ+2λ-12 = 0; 6λ = 12; λ = 2.

Пример 7. Определить угол между векторами a = i + 2j + 3k, b = 6i + 4j - 2k.
Решение: Так как a•b = | a | | b | Cos (a^b) = | a | | b | Cos φ, то Cosφ = a•b/| a | | b |, a•b = 6 + 8 - 6 = 8. | a | = √1+4+9 = √14, | b | = √36+16+4 = √56 = 2√14, Cosφ = 8/√14*2√14 = 2/7, φ = arccos 2/7.