Длиной или модулем вектора называется расстояние между его началом и концом. Записи |АВ| и |a| обозначают модули векторов АВ и a.
Векторы называются коллинеарными, если они параллельны одной прямой, и компланарными, если они параллельны одной плоскости.
Два вектора называются равными, если они коллинеарны, одинаково направлены и равны по длине.
К линейным операциям над векторами относятся:
1) умножение вектора на число (Произведением вектора a и числа α называется вектор, обозначаемый α∙a. (или наоборот a∙α), модуль которого равен |α a| =|α||a|, а направление совпадает с направлением вектора a, если α>0, и противоположно ему, если α< 0.
2) сложение векторов (Суммой векторов 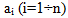 называется вектор, обозначаемый
называется вектор, обозначаемый 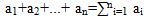 , начало которого находится в начале первого вектора a1, а конец – в конце последнего вектора an, ломаной линии, составленной из последовательности слагаемых векторов. Это правило сложения называется правилом замыкания ломаной. В случае суммы двух векторов оно равносильно правилу параллелограмма)
, начало которого находится в начале первого вектора a1, а конец – в конце последнего вектора an, ломаной линии, составленной из последовательности слагаемых векторов. Это правило сложения называется правилом замыкания ломаной. В случае суммы двух векторов оно равносильно правилу параллелограмма)
Прямая е с заданным на ней направлением, принимаемым за положительное, называется осью е.
Линейной комбинацией векторов ai называется вектор a, определяемый по формуле 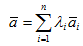 , где
, где 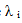 – некоторые числа.
– некоторые числа.
Если для системы n векторов ai равенство
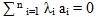
верно только в случае, когда 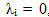 эта система называется линейно независимой. Если же равенство (1) выполняется для
эта система называется линейно независимой. Если же равенство (1) выполняется для 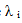 , хотя бы одно из которых отлично от нуля, то система векторов aі называется линейно зависимой. Например, любые коллинеарные векторы, три компланарных вектора, четыре и более векторов в трехмерном пространстве всегда линейно зависимы.
, хотя бы одно из которых отлично от нуля, то система векторов aі называется линейно зависимой. Например, любые коллинеарные векторы, три компланарных вектора, четыре и более векторов в трехмерном пространстве всегда линейно зависимы.
Три упорядочных линейно независимых вектора ē1, ē2, ē3 в пространстве называется базисом. Упорядоченная тройка некомпланарных векторов всегда образует базис. Любой вектор a в пространстве можно разложить по базису ē1, ē2, ē3, т. е. представить a в виде линейной комбинации базисных векторов: a= xē1 + yē2 + zē3, где x, y, z являются координатами вектора a в базисе ē1, ē2, ē3. Базис называется ортонормированным, если его векторы взаимно перпендикулярны и имеют единичную длину. Обозначают такой базис i, j, k, т. е. i=(1, 0, 0), j=(0, 1, 0), k=(0, 0, 1).
Пример 5. Векторы заданы в ортонормированном базисе i, j, k координатами: a=(2;-1;8), е1 = (1,2,3), е2 = (1,-1,-2), е3 = (1,-6,0). Убедиться, что тройка е1,е2,е3 образует базис, и найти координаты вектора 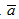 в этом базисе.
в этом базисе.
Решение. Если определитель 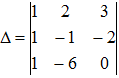 , составленный из координат векторов е1, е2, е3, не равен 0, то векторы е1,е2,е3 линейно независимы и, следовательно, образуют базис. Убеждаемся, что
, составленный из координат векторов е1, е2, е3, не равен 0, то векторы е1,е2,е3 линейно независимы и, следовательно, образуют базис. Убеждаемся, что 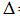 = -18-4+3-12=-31 Таким образом, тройка е1, е2, е3 - базис.
= -18-4+3-12=-31 Таким образом, тройка е1, е2, е3 - базис.
Обозначим координаты вектора a в базисе е1, е2, е3 через x,y,z. Тогда а = (x,y,z) = хе1 + yе2 + zе3. Так как по условию а = 2i – j +8k , е1 = i +2j +3k , е2 = i – j -2k, е3 = i – 6j , то из равенства а = хе1 + yе2 + zе3 следует, что 2i – j +8k = xi + 2xj + 3xk + yi – yj -2yk +zi -6zj = (x+y+z)i +(2x-y-6z)j +(3x-2y)k..Как видно, вектор в левой части полученного равенства равен вектору в правой его части, а это возможно только в случае равенства их соответствующих координат. Отсюда получаем систему для нахождения неизвестных x, y, z:
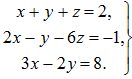
Ее решение: x = 2, y = -1, z = 1. Итак, а = 2е1 – е2 + е3 = (2,-1,1).
|
|
 |
маша 09.01.2013 03:08 полностью согласна))
|