Определение функции: Если каждому числу х из множества чисел D поставлено в соответствие единственное число у, то говорят, что на множестве D задана функция f и пишут y= f(x), где х - называется независимой переменной или аргументом этой функции, а множество D - область определения этой функции.

Все значения, которые принимает функция f(x) (при х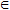D), образуют область значения (изменения) функции Е.

Чтобы задать функцию, нужно указать способ, с помощью которого для каждого значения аргумента можно найти соответствующее значение функции. Существует три способа задания функции: табличный, аналитический, графический.

Табличный способ задания функции состоит в том, что для каждого значения аргумента х рядом выписывается соответствующее значение у, получается таблица. Например:

С точки зрения математики здесь изучается зависимость между определенными переменными, другими словами изучается некоторая функция. При опыте ведутся записи, в простейшем случае отмечается время (аргумент функции) и записывается показание прибора (соответствующее значение функции), т.е. функция задается таблицей. А задача исследователя состоит в том, чтобы по полученной таблице изучить функцию.

Способ задания функции с помощью формулы у=f(х), где f(x) некоторое выражение с переменной х - называется аналитическим способом.

Пример 1. Функция у=f(х) задана аналитической формулой:

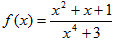
Найти f(-х), f(|х|).
Чтобы найти f(-х), надо в f(х) всюду вместо х подставить (-х). Получим:

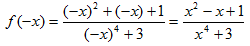. Аналогично находим и для f(|х|).

Пример 2. Найти область определения функции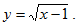

Выражение вида 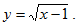определено при тех х, для которых х-10, т.е. при х1
Значит, область определения функции - луч [1,+∞).

Пример 3. Найти области определения и значений функции y=lg(4-3x-x²).

Логарифмическая функция определена, если 4-3x-x²>0. Корни квадратного трехчлена: x₁=-4, x₂=1. Записанное выше неравенство равносильно неравенству -(x+4)(x-1)>0 , что возможно при x>4 и x<1. Область определения данной функции есть интервал (-4;1). Так как в D 0<4-3x-x²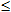25/4, то интервал (-∞ ;lg(25/4)) - область значения функции.

Весьма распространённым, особенно в экспериментальных науках, является графический способ задания функции. Рассмотрим множество F точек координатной плоскости х0у, обладающее следующими свойствами: любая прямая, параллельная оси ординат, пересекает это множество не более чем в одной точке. Пусть множество абсцисс всех точек множества F представляет собой отрезок [a,b]. Возьмем произвольное число х из отрезка[a,b] и проведем через точку х прямую параллельную оси ординат. Эта прямая пересекает F в точке М.

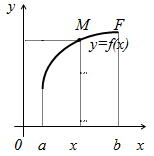
Cпроецировав точку М на ось ординат, найдем число f(x), соответствующее числу х. Тем самым на отрезке задана функция у=f(x).

Определение: Графиком функции y=f(x) называется множество точек F(x,y) плоскости Oxy, координаты которых удовлетворяют функциональной зависимости y=f(x).
Удобнее всего изучать функцию, заданную и аналитически и графически (по заданной формуле строится график). На практике для построения графика функции составляют таблицу значений функций при некоторых значениях аргумента, наносят на плоскость соответствующие точки и соединяют их плавной линией.

Определение: Если функция u=φ(x) определена на области D, G - область ее значений, функция y=f(u) определена на области G, то функция y=f(φ(x))=T(x) называется сложной функцией, составленной из функции f и φ, или функцией f от функции φ. Функцию y=f(φ(x)) называют композицией двух функций y=f(u) и u=φ(x).

Сложная функция может быть композицией большего числа функций: трех, четырех и т.д. Например, функция y=cos(x²+1) - композиция двух функций y=cosu и u=x²+1; функция y=lg(sin2^x) - композиция трех функций.

К основным элементарным функциям относятся пять классов функций: степенные, показательные, логарифмические, тригонометрические и обратные тригонометрические.