1) 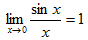; (Первый замечательный предел)

2) 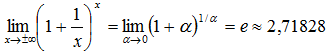(Второй замечательный предел)

Данный предел относят обычно к неопределенностям вида 1^∞. Раскрытие подобных неопределенностей как правило, связано с использованием второго замечательного предела.

Пример 10. Найти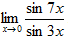

Так как x≠0 под знаком предела, то

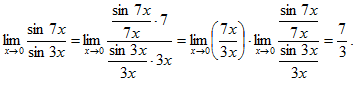
Пример 11. Вычислить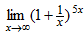

Находим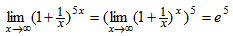

Пример 12 Найти предел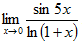

Поскольку sin5x≈5x,ln(1+x)≈x при x→x₀, то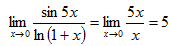

Функция y=f(x) называется непрерывной при x=x₀ (в точке x₀), если:
1) функция f(x) определена в точке x₀ и ее окрестности;
2) существует конечный предел функции f(x) в точке x₀;
3) этот предел равен значению функции в точке x₀ .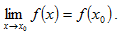
Точка x₀, в которой нарушено хотя бы одно из трех условий непрерывности функции, называется точкой разрыва функции. Если в точке x₀ существуют конечные пределы f(x₀-0) и f(x₀+0) , такие, что f(x₀-0)≠f(x₀+0), то x₀ называется точкой разрыва первого рода. Если хотя бы один из пределов f(x₀-0) и f(x₀+0) не существует или равен бесконечности, то точку x₀ называют точкой разрыва второго рода. Если f(x₀-0)=f(x₀+0) и функция f(x) не определена в точке x₀ или определена, но f(x)≠f(x₀-0)=f(x₀+0), то точку x₀ называют устранимой точкой разрыва функции. 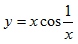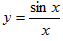Например, для функций и точка x=0 является устранимой точкой разрыва.