Основная задача дифференциального исчисления состоит в нахождении дифференциала данной функции или ее производной. Интегральное исчисление решает обратную задачу: по заданному дифференциалу, а следовательно, и производной неизвестной функции F(x), требуется определить эту функцию. Иными словами, имея выражение:

или соответственно

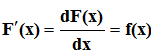
где f(x) – известная функция, нужно найти функцию F(x).
Искомая функция F(x) называется при этом первообразной функцией по отношению к функции f(x).

Первообразной функцией для данной функции f(x) на данном промежутке называется такая функция F(x), производная которой равна f(x) или дифференциал которой равен f(x)dx на рассматриваемом промежутке.

Например, одной из первообразных функций для функции 3х² будет х³ , ибо (х³ )' = 3х² . Первообразная функция не единственна, так как (х³ +1)' = 3х², (x³–5)' = 3х² и т.п., и поэтому функции х³+1, х3 –5 и т.п. также являются первообразными для функции 3х2.

Следовательно, данная функция имеет бесчисленное множество первообразных. Если функция F(x) является первообразной для f(x), то выражение F(x)+C называется неопределенным интегралом от функции f(x) и обозначается символом ∫f(x)dx.

Таким образом, по определению, ∫f(x)dx = F(x)+C, если F'(x) = f(x). При этом функцию f(x) называют подынтегральной функцией, f(x)dx - подынтегральным выражением, знак ∫ – знаком интеграла.

Нахождение первообразной для данной функции f(x) называется интегрированием функции f(x).