Число b называется пределом последовательности у₁, у₂, у₃,…,у_n…,если по мере возрастания номера n член уn неограниченно приближается к b.

Запись 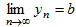Значит n → ∞ подчеркивает, что номер n неограниченно возрастает («стремится к бесконечности»).

Пример 4. Рассмотрим последовательность у₁=0,3; у₂=0,33; у₃=0,333, … уn неограниченно приближается к 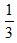(десятичные дроби дают все точные выражения дроби 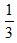). Стало быть, 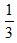есть предел последовательности .

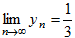Замечание. Разность у_n -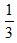 последовательно равна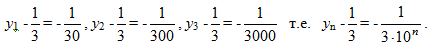

Неограниченность приближения у_n к 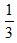выражается в том, что абсолютная величина разности, начиная с некоторого номера N, остается меньше любого (заранее заданного) числа e. Так, если задать e=0,01, то N=2; т.е. начиная со второго номера, абсолютная величина |у_n -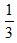| остается меньшей 0,01. Если задать e=0,005, то по-прежнему N=2. Если e=0,001, то N=3; e=0,00001, то N=5 и т.д. Теперь будет понятно следующее определение предела:

Число b называется пределом последовательности у₁, у₂, у₃,… уn,…, если абсолютная величина разности у_n - b, начиная с некоторого номера N, остается меньшей любого заранее данного положительного числа e:
|у_n -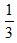|N (номер N зависит от e).

Если b – предел последовательности , то это записывается так: 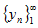. Последовательность, имеющая предел, называется сходящейся, в противном случае – расходящейся.