Материалы по теме: полное приращение, частное приращение, функция, лекция по высшей математики, полный дифференциал, высшая математика

Приращение, которое получает функция Z=f(x, y), когда изменяется только одна из переменных, называется частным приращением функции по соответствующей переменной: ΔxZ=f(x+Δx,y)-f(x,y), ΔyZ=f(x,y+Δy)-f(x,y). ОПРЕДЕЛЕНИЕ: Частным дифференциалом по х функции Z=f(x, y) называется главная часть частного приращения ΔxZ=f(x+Δx,y)-f(x,y), пропорциональная приращению Δx независимой переменной х. Аналогично определяется частный дифференциал по у, т.е. ΔyZ=f(y+Δy,x)-f(x,y). Дифференциалы независимых переменных х и у просто равны их приращениям, т.е. dx=Δx, dy=Δy. Частные дифференциалы обозначаются так: dxZ -частный дифференциал по х, dyZ - частный дифференциал по у. 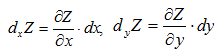При этом: Таким образом, частный дифференциал функции двух независимых переменных равен произведению соответствующей частной производной на дифференциал этой переменной. Таким же образом, как для функции двух переменных, определяются частные приращения и частные дифференциалы функций любого числа независимых переменных. Приращение, которое получает функция Z=f(x,y) при произвольных совместных изменениях ее обоих аргументов называется полным приращением: ΔZ=f(x+Δx,y+Δy)-f(x,y) ОПРЕДЕЛЕНИЕ: Полным дифференциалом функции двух переменных называется главная часть полного приращения функции, линейная относительно приращений независимых переменных. Теорема. Полный дифференциал функции двух независимых переменных равен сумме произведений частных производных функции на дифференциалы соответствующих независимых переменных. dZ=f'x(x,y)dx+f'y(x,y)dy или 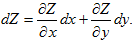Так как dx=dxZ и 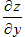dy=dyZ, то dZ=dxZ+dyZ, т.е. дифференциал функции двух независимых переменных равен сумме ее частных дифференциалов. Определение дифференциала переносится на функции любого числа независимых переменных. Пример 7. 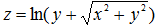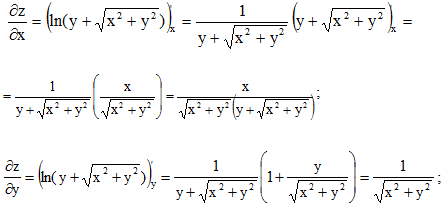Найти dz Найдем частные производные Следовательно,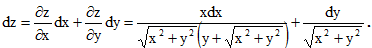

1 2 3 4 5   01.08.2010     6418     4.0/4     1     Артем   Теги: полное приращение, частное приращение, функция, лекция по высшей математики, полный дифференциал, высшая математика

Похожие статьи: Таблица простейших неопределенных интегралов Основные методы интегрирования Определенный интеграл Основные свойства определенного интеграла Формула Ньютона – Лейбница Замена переменной в определенном интеграле Формула интегрирования по частям в определенном интеграле

0   1 Артем   (14.05.2011 19:14) Пример очень помог, на дом дали точь в точь такой же=) спасибо огромное=) Ответить

Имя *:

Код *: