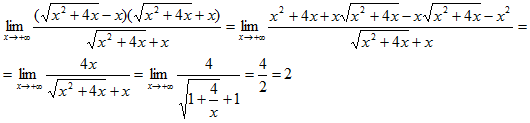Определение: Число b называется пределом функции y=f(x) при х → а, если, по мере того как x, приближается к а – будь то справа или слева значение f(x) неограниченно приближается к b.

Запись: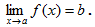

Основные свойства предела функции в точке
I. Если функция имеет предел при х → а, то только один.
II. Если функция имеет предел при х → а, то она ограничена в некоторой окрестности точки a.
III. Если существует 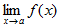и С-постоянная функция (число), то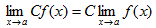
IV. Пусть 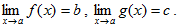, тогда:
1)
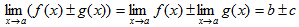
2)
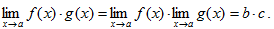
3)

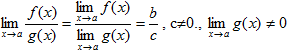
Если условия этих теорем не выполняются, то могут возникнуть неопределенности вида 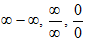и др., которые в простейших случаях раскрываются с помощью алгебраических преобразований.

Пример 5. Вычислить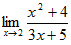

Используя свойства предела, получим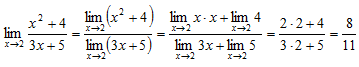

Пример 6. Найти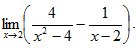

Имеем неопределенность вида 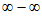. Чтобы раскрыть ее, приведем выражение в скобках к общему знаменателю. Получим 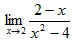, т.е. неопределенность вида 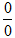, которая легко раскрывается, если под знаком предела сократить дробь на общий множитель x-2≠0. В итоге исходный предел сводится к .

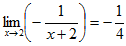Пример 7. Найти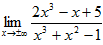

Имеем неопределенность вида 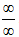. Чтобы раскрыть ее, разделим числитель и знаменатель дроби под знаком предела на x³. Получим 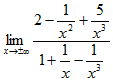. Знаменатель полученной дроби при х → ±∞ не равен нулю, следовательно, можно применить теорему о пределе частного. Также применимы и другие теоремы о пределах, что в итоге приводит к равенству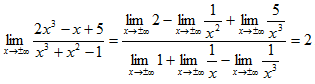

Пример 8. Вычислить предел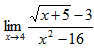

Здесь имеем неопределенность вида 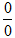. Для её раскрытия умножим числитель и знаменатель на выражение, сопряженное числителю, что позволит избавится от иррациональности в числителе, а затем сократим дробь. Получим:

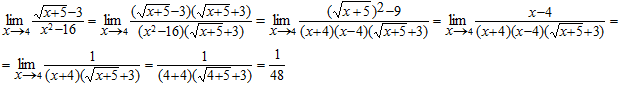
Пример 9. Найти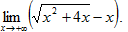

Данное выражение умножим и разделим на сопряженное выражение 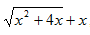, тогда получим: