Формула интегрирования по частям в определенном интеграле
ТЕОРЕМА. Пусть функции u=u(x) и v=v(x) имеют непрерывные производные на отрезке [а,b]. Тогда
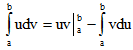 (4)
(4)
где 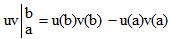
Формула (4) называется формулой интегрирования по частям для определенного интеграла.
Пример 22. Вычислить 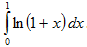
Пусть u=ln(1+x),dv=dx Тогда du=d(ln(1+x))=(ln(1+x))'dx=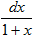 и v=∫dv=∫dx=x. Применяя (4), получаем
и v=∫dv=∫dx=x. Применяя (4), получаем 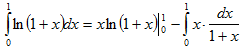
Для нахождения полученного интеграла положим 1+х=t. Тогда dx=dt, x=t-1 и если х=0, то t=1, если x=1, то t=2. Следовательно,
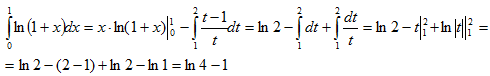
Пример 23. Вычислить
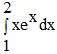
Положим u=x, dv=exdx, отсюда du=dx, v=ex и по формуле (4) имеем:
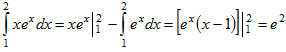
Пример 24. Вычислить 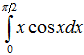
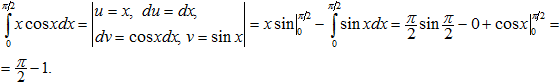
Пример 25. Вычислить 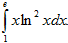
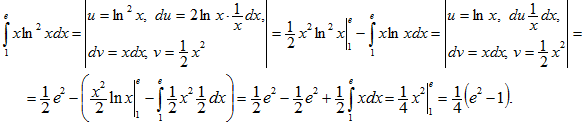
Поиск на сайте
