При введении понятия определенного интеграла мы исходили из условий ограниченности подынтегральной функции и конечности пределов интегрирования. Такой интеграл называется собственным ( слово «собственный» обычно опускается). Если хотя бы одно из этих двух условия невыполнено, то интеграл называется несобственными.

1. Интегралы с бесконечными пределами.
Пусть функция f(x) непрерывна при a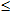x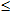∞, т. е. для x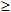a. Тогда по определению полагают

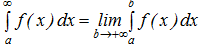(5)

Если последний предел существует, то говорят, что интеграл

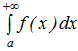(6)

сходится, а если этот предел не существует, то интеграл (6) называется расходящимся. Такому интегралу не приписывают никакого значения.

Пример 26. 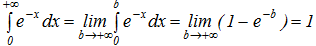. Заданный несобственный интеграл сходится.

Пример 27. 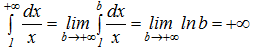. Данный интеграл расходится.

Пример 28. 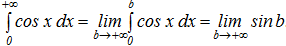. Последний предел не существует, т.е. несобственный интеграл расходится.

На несобственные интегралы вида (6) непосредственно распространяются многие свойства собственных интегралов. Пусть F(x) первообразная функция для подынтегральной функции f(x) сходящегося интеграла (6). На основании формулы (5) и формулы Ньютона –Лейбница имеем: .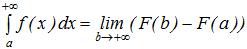

Если ввести условное обозначение 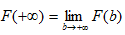, то получим для сходящегося несобственного интеграла (6) обобщенную формулу Ньютона-Лейбница

,

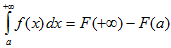которую записывают также в виде