Обозначим это разбиение через τ, a точки x0, x1,…,xn будем называть точками разбиения. В каждом из полученных частичных отрезков [xi-1,xi] выберем произвольную точку ξi(xi-1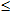 ξi
ξi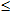 xi). Через Δxi обозначим разность xi-xi-1, которую условимся называть длиной частичного отрезка [xi-1, xi].
xi). Через Δxi обозначим разность xi-xi-1, которую условимся называть длиной частичного отрезка [xi-1, xi].
Образуем сумму:
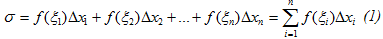
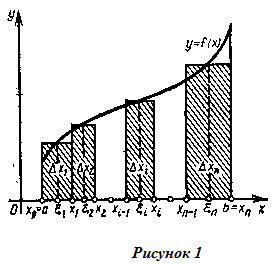
которую назовем интегральной суммой для функции f(x) на [a,b], соответствующее данному разбиению [a,b] на частичные отрезки и данному выбору промежуточных точек ξi. Геометрический смысл суммы σ очевиден: это сумма площадей прямоугольников с основаниями Δx1, Δx2, … , Δxn и высотами f(ξi), f(ξ2), … , f(ξn) (рис 1) (если f(x)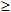 0).
0).
Обозначим через λ длину наибольшего частичного отрезка разбиения τ: 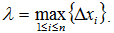
ОПРЕДЕЛЕНИЕ. Если существует конечный предел I интегральной суммы (1) при λ→0, то этот предел называется определенным интегралом от функции f(x) по отрезку [a, b] и обозначается следующим образом:
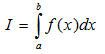
В этом случае функция f(x) называется интегрируемой на [a, b]. Числа a и b называются соответственно нижним и верхним пределами интегрирования, f(x) – подынтегральной функцией, х – переменной интегрирования.
