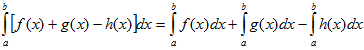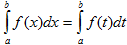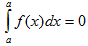
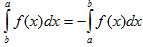
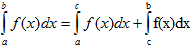
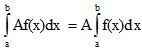
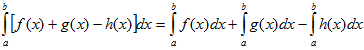
I. Величина определенного интеграла не зависит от обозначения переменной интегрирования, т.е. 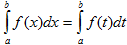, где х, t – любые буквы.

II. Определенный интеграл с одинаковыми пределами интегрирования равен нулю.

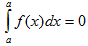
III. При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный.

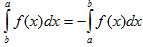
IV. Если промежуток интегрирования [a,b] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутке [a,b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам.

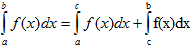
V. Постоянный множитель можно выносить за знак определенного интеграла.

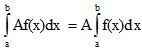
VI. Определенной интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций.