Если функция y=f(x) непрерывна на отрезке [a,b], а ее производная положительна или равна 0 на интервале (a,b), то y=f(x) возрастает на [a,b] (f'(x) 0). Если функция y=f(x) непрерывна на отрезке [a,b], а ее производная отрицательна или равна 0 на интервале (a,b), то y=f(x) убывает на [a,b] (f'(x)
0). Если функция y=f(x) непрерывна на отрезке [a,b], а ее производная отрицательна или равна 0 на интервале (a,b), то y=f(x) убывает на [a,b] (f'(x)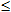 0)
0)
Интервалы, в которых функция не убывает или не возрастает, называются интервалами монотонности функции. Характер монотонности функции может изменяться только в тех точках ее области определения, в которой меняется знак первой производной. Точки, в которых первая производная функции обращается в нуль или терпит разрыв, называются критическими.
Теорема 1 (1-ое достаточное условие существования экстремума).
Пусть функция y=f(x) определена в точке х0 и пусть существует окрестность δ>0 такое, что функция непрерывна на отрезке [x0-δ,x0+δ], дифференцируема на интервале (x0-δ,x0)u(x0, x0+δ), причем ее производная сохраняет постоянный знак на каждом из этих интервалов. Тогда если на x0-δ,x0) и (x0, x0+δ) знаки производной различны, то х0- точка экстремума, а если совпадают, то х0- не является точкой экстремума. При этом если при переходе через точку х0, производная меняет знак с плюса на минус (слева от х0 выполняется f'(x)>0, то х0- точка максимума; если же производная меняет знак с минуса на плюс (справа от х0 выполняется f'(x)<0, то х0- точка минимума.
Точки максимума и минимума называют точками экстремума функции, а максимумы и минимумы функции – ее экстремальными значениями.
Теорема 2 (необходимый признак локального экстремума).
Если функция y=f(x) имеет в токе x=x0 экстремум, то либо f’(x0)=0, либо f’(x0) не существует.
В точках экстремума дифференцируемой функции касательная к ее графику параллельна оси Ox.
Алгоритм исследования функции на экстремум:
1)Найти производную функции.
2)Найти критические точки, т.е. точки, в которых функция непрерывна, а производная равна нулю или не существует.
3)Рассмотреть окрестность каждой из точек, и исследовать знак производной слева и справа от этой точки.
4)Определить координаты экстремальных точек, для этого значения критических точек подставить в данную функцию. Используя достаточные условия экстремума, сделать соответствующие выводы.
Пример 18. Исследовать на экстремум функцию у=х3-9х2 +24х
Решение.
1) y'=3x2-18x+24=3(x-2)(x-4).
2) Приравняв производную нулю, находим x1=2, x2=4. В данном случае производная определена всюду; значит, кроме двух найденных точек, других критических точек нет.
3) Знак производной y'=3(x-2)(x-4) изменяется в зависимости от промежутка так, как показано на рисунке 1. При переходе через точку x=2, производная меняет знак с плюса на минус, а при переходе через точку x=4 - с минуса на плюс.
4) В точке x=2 функция имеет максимум ymax=20, а в точке x=4 - минимум ymin=16.
Теорема 3. (2-ое достаточное условие существование экстремума).
Пусть f'(x0) и в точке х0 существует f''(x0). Тогда если f''(x0)>0, то х0 – точка минимума, а если f''(x0)<0, то х0 – точка максимума функции y=f(x).
На отрезке [a; b] функция y=f(x) может достигать наименьшего (унаим) или наибольшего (унаиб) значения либо в критических точках функции, лежащих в интервале (а;b), либо на концах отрезка [a;b].
Алгоритм отыскания наибольшего и наименьшего значений непрерывной функции y=f(x) на отрезке [a;b]:
1) Найти f'(x).
2) Найти точки, в которых f'(x)=0 или f'(x) - не существует, и отобрать из них те, которые лежат внутри отрезка [a;b].
3) Вычислите значение функции y=f(x) в точках, полученных в п.2), а так же на концах отрезка и выбрать из них наибольшее и наименьшее: они и являются соответственно наибольшим (унаиб) и наименьшим (унаим) значениями функции на отрезке [a;b].
Пример 19. Найти наибольшее значение непрерывной функции y=x3-3x2-45+225 на отрезке [0;6].
1) Имеем y'=3x2-6x-45 на отрезке [0;6]
2) Производная y' существует при всех х. Найдем точки, в которых y'=0; получим:
3x2-6x-45=0
x2-2x-15=0
x1=-3; x2=5
3) Вычислим значение функции в точках x=0 y=225, x=5 y=50, x=6 y=63
Отрезку [0;6] принадлежит лишь точка x=5. Наибольшим из найденных значений функции является 225, а наименьшим – число 50. Итак, унаиб=225, унаим=50.
Исследование функции на выпуклости
На рисунке изображены графики двух функций. Первый из них обращен выпуклостью вверх, второй – выпуклостью вниз.
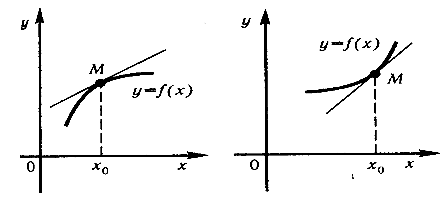
Функция y=f(x) непрерывна на отрезке [a;b] и дифференцируема в интервале (а;b), называется выпуклой вверх (вниз) на этом отрезке, если при a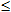 x
x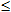 b ее график лежит не выше (не ниже) касательной, проведенной в любой точке M0(x0;f(x0)), где a
b ее график лежит не выше (не ниже) касательной, проведенной в любой точке M0(x0;f(x0)), где a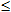 x
x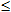 b.
b.
Теорема 4. Пусть функция y=f(x) имеет вторую производную в любой внутренней точке х отрезка [a;b] и непрерывна на концах этого отрезка. Тогда если на интервале (а;b) выполняется неравенство f''(x) 0, то функция выпукла вниз на отрезке [a;b]; если на интервале (а;b) выполняется неравенство f''(x)
0, то функция выпукла вниз на отрезке [a;b]; если на интервале (а;b) выполняется неравенство f''(x)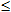 0, то функция выпукла вверх на [a;b].
0, то функция выпукла вверх на [a;b].
Теорема 5. Если функция y=f(x) имеет вторую производную на интервале (а;b) и если она меняет знак при переходе через точку x0, тогда M(x0;f(x0)) есть точка перегиба.
Правило нахождения точек перегиба:
1) Найти точки, в которых f''(x) не существует или обращается в нуль.
2) Исследовать знак f''(x) слева и справа от каждой найденной на первом шаге точки.
3) На основании теоремы 4 сделать вывод.
Пример 20. Найти точки экстремума и точки перегиба графика функции y=3x4-8x3+6x2+12.
Имеем f'(x)=12x3-24x2+12x=12x(x-1)2. Очевидно, что f'(x)=0 при x1=0, x2=1. Производная при переходе через точку x=0 меняет знак с минуса на плюс, а при переходе через точку x=1 не меняет знака. Значит, x=0 - точка минимума (уmin=12), а в точке x=1 экстремума нет. Далее, находим 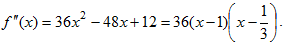 . Вторая производная обращается в нуль в точках x1=1, x2=1/3. Знаки второй производной изменяются следующим образом: На луче (-∞;
. Вторая производная обращается в нуль в точках x1=1, x2=1/3. Знаки второй производной изменяются следующим образом: На луче (-∞;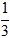 ) имеем f''(x)>0, на интервале (
) имеем f''(x)>0, на интервале (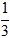 ;1) имеем f''(x)<0, на луче (1;+∞) имеем f''(x)>0. Следовательно, x=
;1) имеем f''(x)<0, на луче (1;+∞) имеем f''(x)>0. Следовательно, x=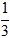 - точка перегиба графика функции (переход с выпуклости вниз на выпуклость вверх) и x=1 - так же точка перегиба (переход с выпуклости вверх на выпуклость вниз). Если x=
- точка перегиба графика функции (переход с выпуклости вниз на выпуклость вверх) и x=1 - так же точка перегиба (переход с выпуклости вверх на выпуклость вниз). Если x=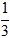 , то y=
, то y=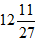 ; если , то x=1, y=13.
; если , то x=1, y=13.
Алгоритм отыскания асимптоты графика
I. Если y=f(x) при x → a 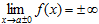 , то x=a - есть вертикальная асимптота.
, то x=a - есть вертикальная асимптота.
II. Если y=f(x) при x → ∞ или x → -∞ 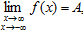 , тогда у=А - горизонтальная асимптота.
, тогда у=А - горизонтальная асимптота.
III. Для нахождения наклонной асимптоты используем следующий алгоритм:
1) Вычислить 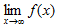 . Если предел существует и равен b, то y=b - горизонтальная асимптота; если
. Если предел существует и равен b, то y=b - горизонтальная асимптота; если 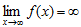 , то перейти ко второму шагу.
, то перейти ко второму шагу.
2) Вычислить 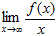 . Если этот предел не существует, то асимптоты нет; если он существует и равен k, то перейти к третьему шагу.
. Если этот предел не существует, то асимптоты нет; если он существует и равен k, то перейти к третьему шагу.
3) Вычислить 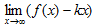 . Если этот предел не существует, то асимптоты нет; если он существует и равен b, то перейти к четвертому шагу.
. Если этот предел не существует, то асимптоты нет; если он существует и равен b, то перейти к четвертому шагу.
4) Записать уравнение наклонной асимптоты y=kx+b.
Пример 21: Найти асимптоту для функции 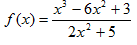
1) 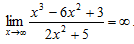
2) 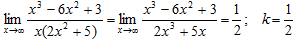
3) 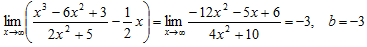
4) Уравнение наклонной асимптоты имеет вид 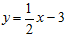
Схема исследования функции и построение ее графика
I. Найти область определения функции.
II. Найти точки пересечения графика функции с осями координат.
III. Найти асимптоты.
IV. Найти точки возможного экстремума.
V. Найти критические точки.
VI. С помощью вспомогательного рисунка исследовать знак первой и второй производных. Определить участки возрастания и убывания функции, найти направление выпуклости графика, точки экстремумов и точек перегиба.
VII. Построить график, учитывая исследование, проведенное в п.1-6.
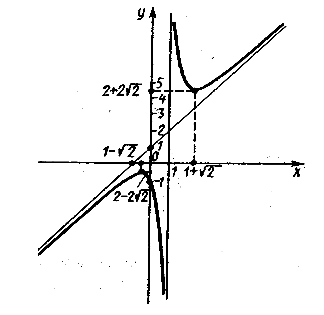
Пример 22: Построить по изложенной выше схеме график функции 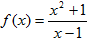
Решение.
I. Областью определения функции является множество всех вещественных чисел, кроме x=1.
II. Так уравнение x2+1=0 не имеет вещественных корней, то график функции не имеет точек пересечения с осью Ох, но пересекает ось Оу в точке (0;-1).
III. Выясним вопрос о существовании асимптот. Исследуем поведение функции вблизи точки разрыва x=1. Так как y → ∞ при х → -∞, у → +∞ при х → 1+, то прямая x=1 является вертикальной асимптотой графика функции.
Если х → +∞(x → -∞), то у → +∞(y → -∞); следовательно, горизонтальной асимптоты у графика нет. Далее, из существования пределов
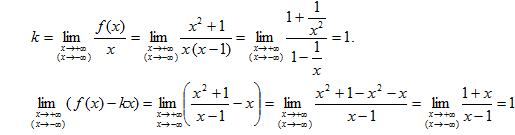
Решая уравнение x2-2x-1=0 получаем две точки возможного экстремума:
x1=1-√2 и x2=1+√2
V. Для нахождения критических точек вычислим вторую производную:
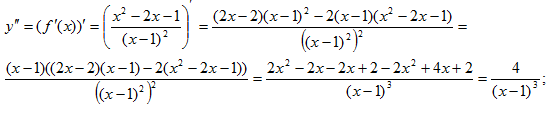
Так как f''(x) в нуль не обращается, то критических точек нет.
VI. Исследуем знак первой и второй производных. Точки возможного экстремума, подлежащие рассмотрению: x1=1-√2 и x2=1+√2, разделяют область существования функции на интервалы (-∞;1-√2),(1-√2;1+√2) и (1+√2;+∞).
В каждом из этих интервалов производная сохраняет знак: в первом – плюс, во втором – минус, в третьем – плюс. Последовательность знаков первой производной запишется так: +,-,+.
Получаем, что функция на (-∞;1-√2) возрастает, на (1-√2;1+√2) убывает, а на (1+√2;+∞) снова возрастает. Точки экстремума: максимум при x=1-√2, причем f(1-√2)=2-2√2 минимум при x=1+√2, причем f(1+√2)=2+2√2. На (-∞;1) график направлен выпуклостью вверх, а на (1;+∞) - вниз.
VII Составим таблицу полученных значений
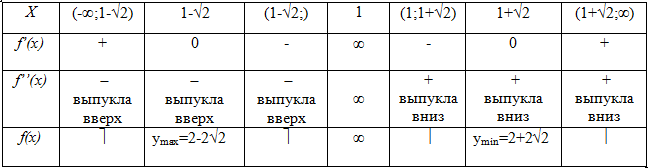
VIII По полученным данным строим эскиз графика функции