Логарифмическое дифференцирование
Логарифмической производной функции y=f(x) называется производная от логарифма этой функции, т.е.
(ln f(x))'=f'(x)/f(x)
Последовательное применение логарифмирования и дифференцирования функций называют логарифмическим дифференцированием. В некоторых случаях предварительное логарифмирование приводит к формуле:
y'=uv•ln u•v'+vuv-1•u'
Пример 17. Найти производную функции y=(sin2x)x3
Логарифмируя данную функцию, получаем ln y=x3•ln sin2x. Дифференцируем обе части последнего равенства по x: (ln y)'=(x3)'•ln sin2x+x3(ln sin2x)'. Отсюда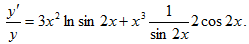 
. Далее, y'=y(3x2ln sin2x+2x3ctg2x). Окончательно имеем: y'=(sin2x)x3(3x2ln sin2x+2x3ctg2x)