Правило Лопиталя
Правило Лопиталя (для раскрытия неопределенностей вида 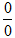 и
и 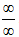 )
) 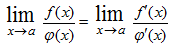
Если частное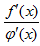 вновь дает в предельной точке неопределенность одного их двух названных видов и функции f'(x); φ'(х) удовлетворяют всем требованиям, раннее указанным для функций f(х) и у=φ(х), то можно перейти к отношению вторых производных и т.д. Однако следует помнить, что предел отношения самих функций может существовать, в то время как отношение производных не стремится ни к какому пределу.
вновь дает в предельной точке неопределенность одного их двух названных видов и функции f'(x); φ'(х) удовлетворяют всем требованиям, раннее указанным для функций f(х) и у=φ(х), то можно перейти к отношению вторых производных и т.д. Однако следует помнить, что предел отношения самих функций может существовать, в то время как отношение производных не стремится ни к какому пределу.
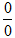 и
и 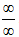 )
) Если функции у=f(x) и у=φ(х) дифференцируемы в некоторой окрестности точки х=а, стремятся к нулю (или ±∞) при х → а и существует 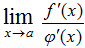 то справедливо следующее:
то справедливо следующее:
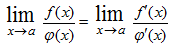
Если частное
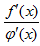 вновь дает в предельной точке неопределенность одного их двух названных видов и функции f'(x); φ'(х) удовлетворяют всем требованиям, раннее указанным для функций f(х) и у=φ(х), то можно перейти к отношению вторых производных и т.д. Однако следует помнить, что предел отношения самих функций может существовать, в то время как отношение производных не стремится ни к какому пределу.
вновь дает в предельной точке неопределенность одного их двух названных видов и функции f'(x); φ'(х) удовлетворяют всем требованиям, раннее указанным для функций f(х) и у=φ(х), то можно перейти к отношению вторых производных и т.д. Однако следует помнить, что предел отношения самих функций может существовать, в то время как отношение производных не стремится ни к какому пределу.
|
|
 |
Виктор 05.04.2011 22:55 ничего не понимаю
 |
Поиск на сайте
