ОПРЕДЕЛЕНИЕ: Если существует предел 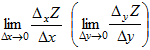 , то он называется частной производной функции Z=f(M) в точке М по переменной х (по переменной у) и обозначается одним из следующих символов:
, то он называется частной производной функции Z=f(M) в точке М по переменной х (по переменной у) и обозначается одним из следующих символов: 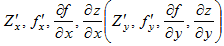
Из определения следует, что частная производная функции двух переменных по переменной х представляет собой обыкновенную производную функции одной переменной х при фиксированном значении переменной у. Поэтому частные производные вычисляют по формулам и правилам вычисления производных функции одной переменной.
Пример 3. Найти частные производные функции Z=x2-2xy2+y3
Частную производную  находим как производную функции Z=f(x,y) по аргументу х в предположении, что y=const. Поэтому
находим как производную функции Z=f(x,y) по аргументу х в предположении, что y=const. Поэтому
 =(x2-2xy2+y3)'x=2x-2y2+0=2(x-y2)
=(x2-2xy2+y3)'x=2x-2y2+0=2(x-y2)
Аналогично, 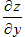 =(x2-2xy2+y3)'y=0-4xy+3y2=y(3y+4x)
=(x2-2xy2+y3)'y=0-4xy+3y2=y(3y+4x)
Пример 4. 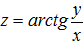 . Найти
. Найти  ,
, 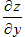
Рассматривая y как постоянную величину, получим:
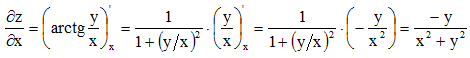
Рассматривая x как постоянную величину, находим:
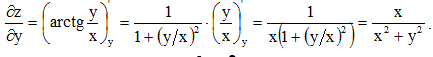
Пример 5. z=xe-xy. Найти  ,
, 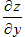
 =(xe-xy)'x=e-xy-xye-xy=e-xy(1-xy)
=(xe-xy)'x=e-xy-xye-xy=e-xy(1-xy)
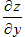 =(xe-xy)'y=-x2e-xy
=(xe-xy)'y=-x2e-xy
Пример 6. 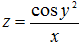 . Найти
. Найти  ,
, 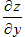
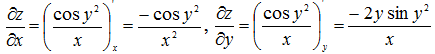
|
|
 |
Диана 10.12.2010 13:26 помогите, пожалуйста, никак не могу решить z=xye, где е в степени xy
|
