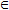Значение функции в точке максимума (минимума) называется максимумом (минимумом) функции. Максимум и минимум функции называют ее экстремумом.

Теорема 1 (необходимые условия экстремума). Если в точке N₀(x₀;y₀) дифференцируемая функция z=f(x,y) имеет экстремум, то ее частные производные в этой точке равны нулю: f'_x(x₀;y₀)=0, f'_y=(x₀;y₀)=0.

Точка в которой частные производные первого порядка функции z=f(x,y) равны нулю, т.е. f'_x=0, f'_y=0, называется стационарной точкой функции z (или точкой возможного экстремума). Стационарные точки и точки, в которых хотя бы одна частная производная не существует называется критическими точками. В критических точках функция может иметь экстремума, а может не иметь. Равенство нулю частных производных является необходимым, но недостаточным условием существования экстремума. Для нахождения экстремумов функции в данной области необходимо критическую точку функции подвергнуть дополнительному исследованию.

Теорема 2 (достаточные условия экстремума). Пусть в стационарной точке N₀(x₀;y₀) и некоторой ее окрестности функция f(x,y) имеет непрерывные частные производные до второго порядка включительно. Вычислим в точке N₀(x₀;y₀) значения A=f'_x'_x(x₀;y₀), B=f'_x'_y(x₀;y₀), C=f'_y'_y(x₀;y₀)Обозначим 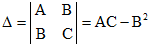. Тогда:

1. Если Δ>0, то функция f(x,y) в точке N₀(x₀;y₀) имеет экстремум: максимум, если A<0: минимум, если A>0.
2. Если Δ<0, то функция f(x,y) в точке N₀(x₀;y₀) экстремума не имеет.
3. В случае Δ=0 экстремум в точке N₀(x₀;y₀) может быть, может не быть. Необходимо дополнительные исследования.

Пример 1. Найти экстремум функции z=3x²y-x³-y⁴

Имеем z'_x=6xy-3x², z'_y=3x²-4y³. Точки, в которых частные производные не существуют, отсутствуют. Найдем стационарные точки, решая систему уравнений:

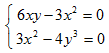
отсюда получаем точки M₁(6;3) и M₂(0;0).
Находим частные производные второго порядка данной функции:
z'_x'_x=6y-6x, z'_x'_y=6x, z'_y'_y=-12y²

В точке M₁(6;3) имеем: A=-18, B=36, C=-108 отсюда
AC-B²=-18•(-108)•-36²=648, т.е. Δ>0

Так как A<0, то в точке M₁(6;3) функция имеет локальный максимум: z_max=z(6;3)-3•36•3-6³-3⁴=27.

В точке M₂(0;0): A=0, B=0, C=0 и значит, Δ=0. Проведем дополнительное исследование. Значение функции z в точке M₂ равно нулю: z(0;0)=0. Можно заметить, что z=-y⁴<0 при x=0, y≠0: z=-x³>0 при x≠0, y=0. Значит, в окрестности точки M₂(0;0) функция z принимает как отрицательные, так и положительные значения. Следовательно, в точке M₂ функция экстремума не имеет.