Материалы по теме: интеграл, функция, определенный интеграл, лекция по высшей математики, формула, высшая математика

Основной формулой интегрального исчисления является так называемая формула Ньютона-Лейбница. ТЕОРЕМА. Пусть функция у=f(x) непрерывна на отрезке [a,b] и F(x) – любая первообразная для f(x) на [a,b]. Тогда определенный интеграл от функции f(x) на [a,b] равен приращению первообразной F(x) на этом отрезке, т.е. 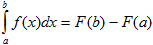(2) Нахождение определенных интегралов с использованием формулы Ньютона–Лейбница (2) осуществляется в два шага: на первом шаге, используя технику нахождения неопределенного интеграла, находят некоторую первообразную F(x) для подынтегральной функции f(x); на втором применяется собственно формула Ньютона-Лейбница – находится приращение первообразной, равное искомому интегралу. В связи с этим, введем обозначение для приращения первообразной, которое удобно использовать при записи решений. По определению положим 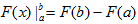(3) Следует подчеркнуть, что при применении формулы Ньютона – Лейбница можно использовать любую первообразную F(x) для подынтегральной функции f(x), например имеющую наиболее простой вид при С=0. Пример 16: Вычислить определенный интеграл 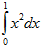Произвольная первообразная для функции f(x)=x2 имеет вид 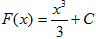. Для нахождения интеграла по формуле Ньютона – Лейбница возьмем такую первообразную, у которой С=0. Тогда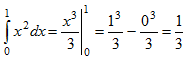 Пример 17. 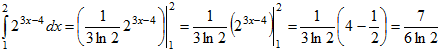Пример 18. Вычислить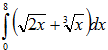

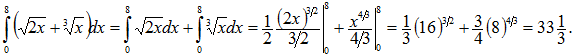
1 2 3 4 5   31.07.2010     3526     5.0/2     1     Артем   Теги: интеграл, функция, определенный интеграл, лекция по высшей математики, формула, высшая математика

Похожие статьи: Интегральное исчисление функции одной переменной Основные методы интегрирования Определенный интеграл Основные свойства определенного интеграла Замена переменной в определенном интеграле Формула интегрирования по частям в определенном интеграле Несобственные интегралы

0   1 сергей   (21.04.2011 09:20) мне нужна история возникновения формулы ньютона-лейбница. где искать? Ответить

Имя *:

Код *: