a) Случай двух независимых переменных.
Остановимся сначала в случае двух независимых переменных, которые будем обозначать буквами x и y. Каждой паре значений x и y соответствует точка на плоскости ОХУ, координатами которой они служат.

ОПРЕДЕЛЕНИЕ: Пусть D-некоторое множество точек на плоскости Оху. Величина Z называется функцией переменных величин x и y на множестве D, если каждой точке этого множества соответствует одно определенное значение величины Z и пишут.

Число Z называется значением функции f в точке (х; у). Переменную Z называют зависимой переменной, а переменные x и y – независимыми переменными (или аргументами); множество D – областью определения функции.
Упорядоченная пара значений x и y называется точкой М(х;у), а функция двух переменных - функцией этой точки Z=f(M). Областью определения функции в этом случае является некоторое множество {M} точек плоскости.

Пример 1. Найти область определения функции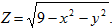

Данная функция определена, если 9-x²-y²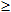0 т.е. x²+y²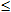9. Этому соотношению удовлетворяют координаты всех точек, которые находятся внутри круга радиуса с центром в начале координат, а также на его границе. Областью определения данной функции и является указанный круг.

Пример 2. Найти область определения функции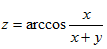

Эта функция определена, если 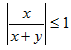, y≠-x, то есть |x|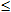|x+y|, y≠-x. Возведя в квадрат обе части предыдущего неравенства, получим x²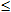x²+2xy+y², то есть 2xy+y²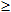0. Далее, имеем 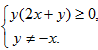. Данная система будет выполняться, если выполняется одно из следующих соотношений 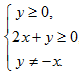либо 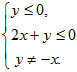, В итоге, область определения функции можно записать в виде .

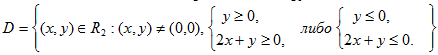Геометрически D состоит из двух тупых углов, образованных прямыми y=0, y=-2x, включая границы без точки (0;0).

b) Случай многих независимых переменных.
Пусть x, y, z,...,t - независимые переменные, а u - величина, зависимая от них.

ОПРЕДЕЛЕНИЕ: Величина u называется функцией переменных величин x, y, z,...,t, если каждой рассматриваемой совокупности этих величин соответствует одно определенное значение величины u и пишут: u=f(x,y,z,...,t).