Материалы по теме: интеграл, функция, лекция по высшей математики, высшая математика

Для вычисления данного интеграла мы должны, если это возможно, пользуясь теми или другими способами, привести его к табличному интегралу и таким образом найти искомый результат. В нашем курсе мы рассмотрим лишь некоторые, наиболее часто встречающиеся приемы интегрирования и укажем их применение к простейшим примерам. Наиболее важными методами интегрирования являются: 1) метод непосредственного интегрирования (метод разложения), 2) метод подстановки (метод введения новой переменной), 3) метод интегрирования по частям. I. Метод непосредственного интегрирования Задача нахождения неопределенных интегралов от многих функций решается методом сведения их к одному из табличных интегралов. Пример 1. ∫(1-√x)2dx=∫(1-2√x+x)dx=∫dx-∫2√xdx+∫xdx=∫dx-2∫xdx+∫xdx=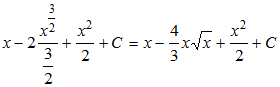 Пример 2. 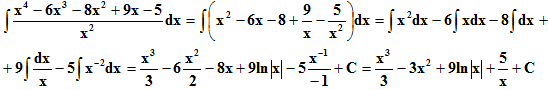Пример 3. ∫sin2xdx Так как sin2x=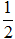(1-cos2x), то ∫sin2xdx=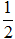(1-cos2x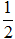)dx=∫dx-∫cos2xd(2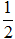x)=x-sin2x+C Пример 4. ∫sinxcos3xdx Так как sinxcos3x=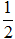(sin4x-sin2x), то имеем ∫sinxcos3xdx=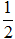∫(sin4x-sin2x)dx=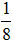∫sin4xd(4x)-∫sin2xd(2x)=-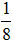cos4x+cos2x+C Пример 5. Найти неопределенный интеграл: ∫cos(7x-3)dx ∫cos(7x-3)=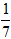∫cos(7x-3)d(7x-3)=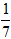sin(7x-3)+C Пример 6. 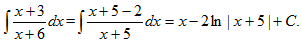II. Метод подстановки (интегрирование заменой переменной) Если функция x=φ(t) имеет непрерывную производную, то в данном неопределенном интеграле ∫f(x)dx всегда можно перейти к новой переменной t по формуле ∫f(x)dx=∫f(φ(t))φ'(t)dt Затем найти интеграл из правой части и вернуться к исходной переменной. При этом, интеграл стоящий в правой части данного равенства может оказаться проще интеграла, стоящего в левой части этого равенства, или даже табличным. Такой способ нахождения интеграла называется методом замены переменной. Пример 7. ∫x√x-5dx Чтобы избавиться от корня, полагаем √x-5=t. Отсюда x=t2+5 и, следовательно, dx=2tdt. Производя подстановку, последовательно имеем: ∫x√x-5dx=∫(t2+5)•2tdt=∫(2t4+10t2)dt=2∫t4dt+10∫t2dt=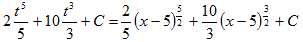 Пример 8. 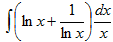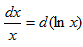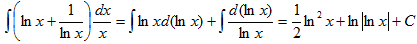Так как , то имеем Пример 9. 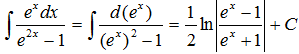Пример 10. ∫e-x3x2dx Воспользуемся подстановкой -x3=t. Тогда имеем -3x2dx=dt и ∫e-x3x2dx=∫et(-1/3)dt=-1/3et+C=-1/3e-x3+C Пример 11. 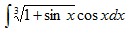Применим подстановку 1+sinx=t , тогда cosxdx=dt и 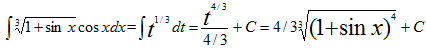III. Метод интегрирования по частям Метод интегрирование по частям основан на следующей формуле: ∫udv=uv-∫vdu где u(x),v(x) –непрерывно дифференцируемые функции. Формула называется формулой интегрирования по частям. Данная формула показывает, что интеграл ∫udv приводит к интегралу ∫vdu, который может оказаться более простым, чем исходный, или даже табличным. Пример 12. Найти неопределенный интеграл ∫xe-2xdx Воспользуемся методом интегрирование по частям. Положим u=x, dv=e-2xdx. Тогда du=dx, v=∫xe-2xdx=-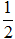e-2x+C Следовательно по формуле имеем: ∫xe-2xdx=x(-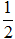e-2x)-∫-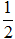-2d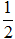x=-e-2x-e-2x+C Пример 13. ∫(x2+2x)cos2xdx u=x2+2x, du=(2x+2)dx, dv=cos2xdx, v=∫cos2xd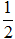x=sin2x ∫(x2+2x)cos2xdx=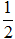(x2+2x)sin2x-∫(x+1)sin2xdx u=x+1, du=dx, dv=sin2xdx, v=-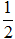cos2x 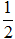(x2+2x)sin2x-∫(x+1)sin2xdx=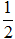(x2+2x)sin2x+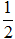(x+1)cos2x+sin2x+C

1 2 3 4 5   31.07.2010     7858     3.6/5     1     Артем   Теги: интеграл, функция, лекция по высшей математики, высшая математика

Похожие статьи: Интегральное исчисление функции одной переменной Первообразная функция. Неопределенный интеграл Основные свойства неопределенного интеграла Таблица простейших неопределенных интегралов Определенный интеграл Формула интегрирования по частям в определенном интеграле Несобственные интегралы

0   1 гранат   (05.09.2011 21:52) отличный сайт Ответить

Имя *:

Код *: