Предел и непрерывность функции двух переменных
Пусть функция Z=f(M) определена на некотором множестве {M} и точка M0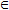 {M} или M0
{M} или M0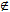 {M}, но обладает тем свойством, что в любой δ-окрестности этой точки содержится хотя бы одна точка множества {M}, отличная от M0.
{M}, но обладает тем свойством, что в любой δ-окрестности этой точки содержится хотя бы одна точка множества {M}, отличная от M0.
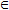 {M} или M0
{M} или M0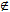 {M}, но обладает тем свойством, что в любой δ-окрестности этой точки содержится хотя бы одна точка множества {M}, отличная от M0.
{M}, но обладает тем свойством, что в любой δ-окрестности этой точки содержится хотя бы одна точка множества {M}, отличная от M0. ОПРЕДЕЛЕНИЕ: Число А называется пределом функции Z=f(M) в точке M0, если функция Z=f(M) определена в окрестности точки M0 и для любого ε>0, δ>0 такое что при |M0M|<δ, выполняется неравенство |f(M)-A|<ε.
обозначение: 
ОПРЕДЕЛЕНИЕ: Функция Z=f(M) называется непрерывной в точке M0, если предел функции в этой точке существует и равен значению функции в этой точке, т.е.
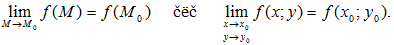
Поиск на сайте
