ТЕОРЕМА. Пусть функция φ(t) имеет непрерывную производную на отрезке [α,β], а=φ(α), в=φ(β) и функция f(х) непрерывна в каждой точке х вида х=φ(t), где t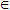 [α,β].
[α,β].
Тогда справедливо следующее равенство:
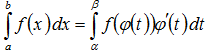
Эта формула носит название формулы замены переменной в определенном интеграле.
Подобно тому, как это было в случае неопределенного интеграла, использование замены переменной позволяет упростить интеграл, приблизив его к табличному (табличным). При этом в отличие от неопределенного интеграла в данном случае нет необходимости возвращаться к исходной переменной интегрирования. Достаточно лишь найти пределы интегрирования α и β по новой переменной t как решение относительно переменной t уравнений φ(t)=а и φ(t)=в. На практике, выполняя замену переменной, часто начинают с того, что указывают выражение t=ψ(х) новой переменной через старую. В этом случае нахождение пределов интегрирования по переменной t упрощается: α=ψ(а), β=ψ(в).
Пример 19. Вычислить 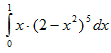
Положим t=2-х2. Тогда dt=d(2-х2)=(2-х2)'dx=-2xdx и xdx=-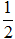 dt. Если х=0, то t=2-02=2, и если х=1, то t=2-12=1. Следовательно:
dt. Если х=0, то t=2-02=2, и если х=1, то t=2-12=1. Следовательно:
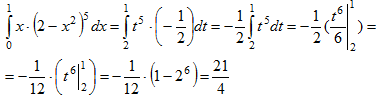
Пример 20. Вычислить 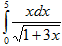
Воспользуемся заменой переменной 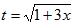 . Тогда
. Тогда 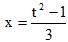 и
и 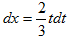 . Если х=0, то t=1 и, если х=5, то t=4. Выполняя замену, получим:
. Если х=0, то t=1 и, если х=5, то t=4. Выполняя замену, получим:
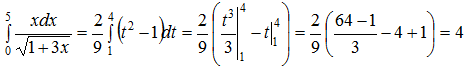
Пример 21. Вычислить 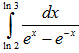
Положим t=ex. Тогда x=lnt, dx=dt/t и, если x=ln2, то t=2, если х=ln3, то t=3. Выполняя замену, получаем:
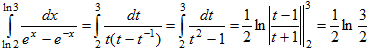
|
|
 |
fff 11.02.2015 02:51 20 пример после тогда что за действие зачем? Тогда ??????
|
|
|
 |
АСЕЛЯ 02.06.2011 23:58 КазГаСа 4-аудитория 1-поток пиште. по географию помогу каз класс
|