С тех пор, как отменили обязательный экзамен по геометрии, этот предмет быстро катился в разряд второстепенных. Алгебра более алгоритмизирована, там есть возможность «натаскивания» школьников на курсах, с помощью репетиторов. С геометрией все гораздо сложнее. Здесь, даже имея большой опыт решения задач, чаще встречаешься с ситуацией «неразгрызаемого орешка». Практика показывает, что многие школьники (даже гимназисты из профильных классов!) не умеют решать задачи геометрии, а особенно — планиметрические задачи.
Планиметрия представляет собой замкнутую модель науки, внутри которой можно бесконечно совершенствоваться. Она дает большие возможности для развития творческого, интеллектуального, создает тот самый развивающий дискомфорт, преодолевая который, ребенок только и может двигаться вперед в своем развитии.
В данном элективном курсе следует выделить два главных направления:
1. Знакомство школьников с основными методами решения задач планиметрии.
2. Решение одной задачи всеми доступными им способами.
Следует особо отметить, что успешность п.2 во многом зависит от самих школьников, от их инициативы и творчества. Поэтому основными формами проведения занятий будут служить практикумы, соревнования, работа в группах, математические бои, дискуссии.
Цели курса:
– научить рассуждать, опираясь на факты;
– научить думать на материале математики;
– научить учить себя.
Требования к знаниям и умениям обучающихся.
После изучения данного элективного курса обучающиеся должны знать и уметь:
• правильно анализировать условия задачи;
• выполнять грамотный чертеж к задаче;
• выбирать наиболее рациональный метод решения;
• в сложных задачах использовать вспомогательные задачи (задачи - спутники);
• логически обосновывать собственное мнение;
• использовать символический язык для записи решений геометрических задач;
• следить за мыслью собеседника; корректно вести дискуссию.
Содержание элективного курса
«Методы решения планиметрических задач»
1. Искусство поиска решения задач (общие рекомендации). Примеры поиска решения. Задачи-спутники, помогающие выбрать нужные знания.
2. Методы решения задач
а. Метод подобия
б. Метод решения задач «с конца»
в. Числовые средние и геометрия
г. Метод координат
д. Использование площадей. Равносоставленность.
е. Наибольшее и наименьшее значения.
ё. Метод геометрических мест.
ж. Метод вспомогательной окружности.
з. Замечательные линии и точки треугольника.
и. Алгебраический метод.
к. Откуда берутся задачи? (Приемы составления задач).
З. Подведение итогов. Что такое КРАСИВАЯ ЗАДАЧА?
Искусство поиска решения задач.
Задачи-спутники, помогающие выбрать нужные знания.
На сегодняшнем занятии мы рассмотрим так называемые «задачи-спутники» и несколько более сложных задач, где их используют. Задачи-спутники легкие, известные вам, но я попрошу все-таки обосновывать подробно каждую из них, чтобы восстановить цепочку знаний. Главная наша цель сегодня – не просто найти доказательства (решение) задачи, но найти логические связи между задачами.
Вспомогательные задачи (задачи-спутники).
А) Доказать, что в прямоугольном треугольнике медиана, проведенная к гипотенузе, равна ее половине.
Б) Где лежит центр окружности, описанной около прямоугольного треугольника, и чему равен ее радиус?
В) Выразить радиус вписанной окружности через гипотенузу и катеты прямоугольного треугольника.
Г) Выразить высоту, проведенную к гипотенузе, через гипотенузу и катеты.
Применение вспомогательных задач.
1. Доказать, что если медиана треугольника равна половине стороны, к которой она проведена, то треугольник – прямоугольный.
2. В треугольнике АВС из вершин А и В проведены высоты, О – середина стороны АВ. Доказать, что отрезки, соединяющее основания высот с точкой О, равны.
3. В параллелограмме из вершины тупого угла проведены высоты, О – точка пересечения диагоналей параллелограмма. Доказать, что отрезки, соединяющие точку О с основаниями высот, равны.
4. В ромб, который делится своей диагональю на два равносторонних треугольника, вписана окружность радиуса r. Найти сторону ромба.
5. Вот треугольник непростой:
В нем угол АВС – прямой.
А теперь – условий узы:
с – длина гипотенузы,
r – величина не меньшей нужности –
Радиус вписанной окружности.
Задача, посильная для школьника –
Найти площадь треугольника!
Обсуждение задач:
Задача А: Дополняем треугольник до прямоугольника и используем свойство его диагоналей. Задача В является следствием задачи А, в ней используется определение окружности и определение окружности, описанной около треугольника.
Задача В (рис. 1) По свойству касательных, проведенных к окружности из одной точки,
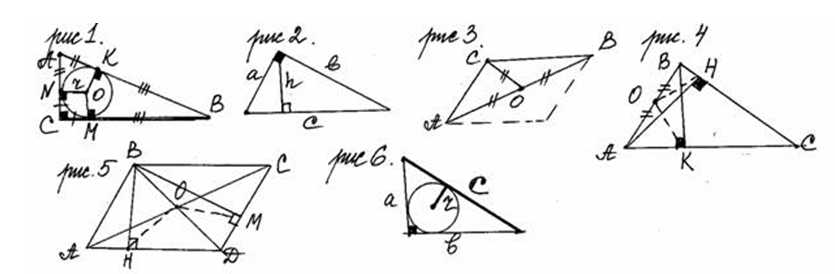
АК = АN, BK = BM, CM = CN. Четырехугольник CMON – квадрат, сторона которого равна r. АN = b – r = АК, ВМ = a – r = BK, АВ = АК + КВ = b – r + a – r = с, отсюда 2r = a + b – c, r = (a + b – c)/2.
Задача Г. Вспомним, как найти площадь прямоугольного треугольника двумя способами: S = ab/2 = ch/2, отсюда h = ab/c (рис.2).
При решении задачи №1 следует обратиться к задаче А (это обратные задачи).
Достроим наш треугольник АВС до параллелограмма (рис.3). Диагонали параллелограмма точкой пересечения делятся пополам, но в нашей задаче половинки АО = ВО = СО, тогда АВ = CD, а это признак прямоугольника, поэтому угол АСВ равен 900.
Задача №2 (рис. 4). Доказать, что ОК = OH.
Опять надо искать некоторую общую идею. Какая это идея? По условию О – середина АВ, значит ищи медиану или медианы! ОК – медиана в треугольнике АВК, ОН – медиана в треугольнике АВН, поэтому ОК = АВ/2 и ОН = АВ/2.
Задача №3 (рис. 5). Доказать, что ОН = ОМ.
Опять надо искать некоторую общую идею. Попробуйте найти прямую связь этой задачи с задачей №2.
Задача №4. Задаем вопросы самому себе: 1) где лежит центр вписанной окружности?
2) Почему в ромб можно вписать окружность?
3) Где провести радиус?
4) Каковы свойства диагоналей ромба?
В итоге всех рассуждений получаем вспомогательную задачу Г: гипотенуза прямоугольного треугольника х (сторона ромба), катеты х/2 и х , высота, проведенная к гипотенузе – r ; r = (x/2 + х - x)/2; Ответ: х = 4r/( - 1).
Задача №5 (рис. 6). При решении этой задачи надо вспомнить все, связанное с площадью треугольника, радиусом вписанной окружности и гипотенузой, потому что сразу решение не просматривается! Итак, вспоминаем: S = ab/2 => 2S = ab; r = (a + b – c)/2 => 2r + c = a + b; необходимо как-то связать произведение чисел ab и их сумму a + b! Где искать эту связь? – Оказывается, в алгебре. Вспомним формулы сокращенного умножения: (a + b)2 = a2 + b2 + 2ab; (2r + c)2 = c2 + 2ab; 2ab = 4r2 + 4rc + c2 – c2;
ab = 2r2 + 2rc; ab/2 = r2 + rc = S. Ответ: S = r2 + rc.
