Материалы по теме: функция, производная, лекция по высшей математики, дифференциал, высшая математика

Пусть функция y=f(x) дифференцируема на множестве Х. Производная f'(x) этой функции является функцией от х на Х. Следовательно, можно говорить о производной полученной функции, т.е. о производной от первой производной. Если она существует, то её называют производной второго порядка функции у= f(x) или , короче, второй производной и обозначают f''(x) или у''. Значит по определению f''(x)=( f' (x))'. Аналогично если существует производная от второй производной, то её называют третьей производной и обозначают f'''(x)=( f''(x))' и т.д. Вообще производной n-го порядка называют производную от производной (n-1)- го порядка 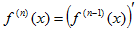и обозначают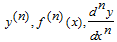 Пример 16. Найдем производную третьего порядка функции y=3x3+1 y'=(3x3+1)'=9x2 y''=(9x2)'=18x y'''=(18x)'=18

1 2 3 4 5   30.07.2010     3903     3.0/2     0     Артем   Теги: функция, производная, лекция по высшей математики, дифференциал, высшая математика

Похожие статьи: Дифференциальное исчисление функции одной переменной Понятие функции Производная функции, её геометрический и физический смысл Логарифмическое дифференцирование Функции многих переменных Частные производные Частные производные и дифференциалы высших порядков

Имя *:

Код *: